- 全部分类/
- 教育教学/
- 数理天地(高中版)
 扫码免费借阅
扫码免费借阅
目录
快速导航-
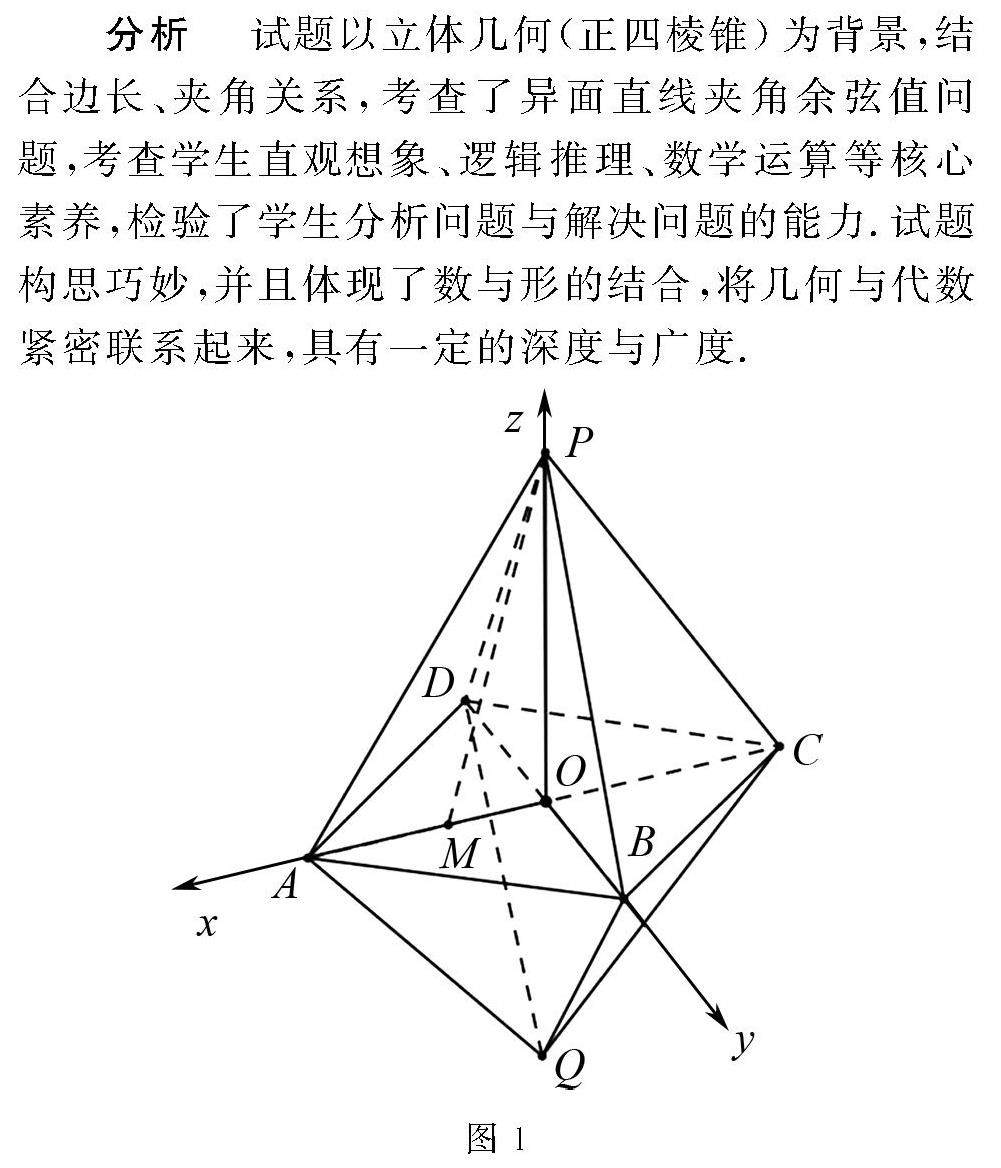
本期推荐 | 2023全国高中数学联合竞赛(预赛B卷)第7题的求解、变式与拓展探究
本期推荐 | 2023全国高中数学联合竞赛(预赛B卷)第7题的求解、变式与拓展探究
-

基础精讲 | 不同类型绝对值不等式问题的解法
基础精讲 | 不同类型绝对值不等式问题的解法
-

基础精讲 | 换底公式的应用
基础精讲 | 换底公式的应用
-

基础精讲 | 例谈巧设问题链促进学生数学思维发展
基础精讲 | 例谈巧设问题链促进学生数学思维发展
-
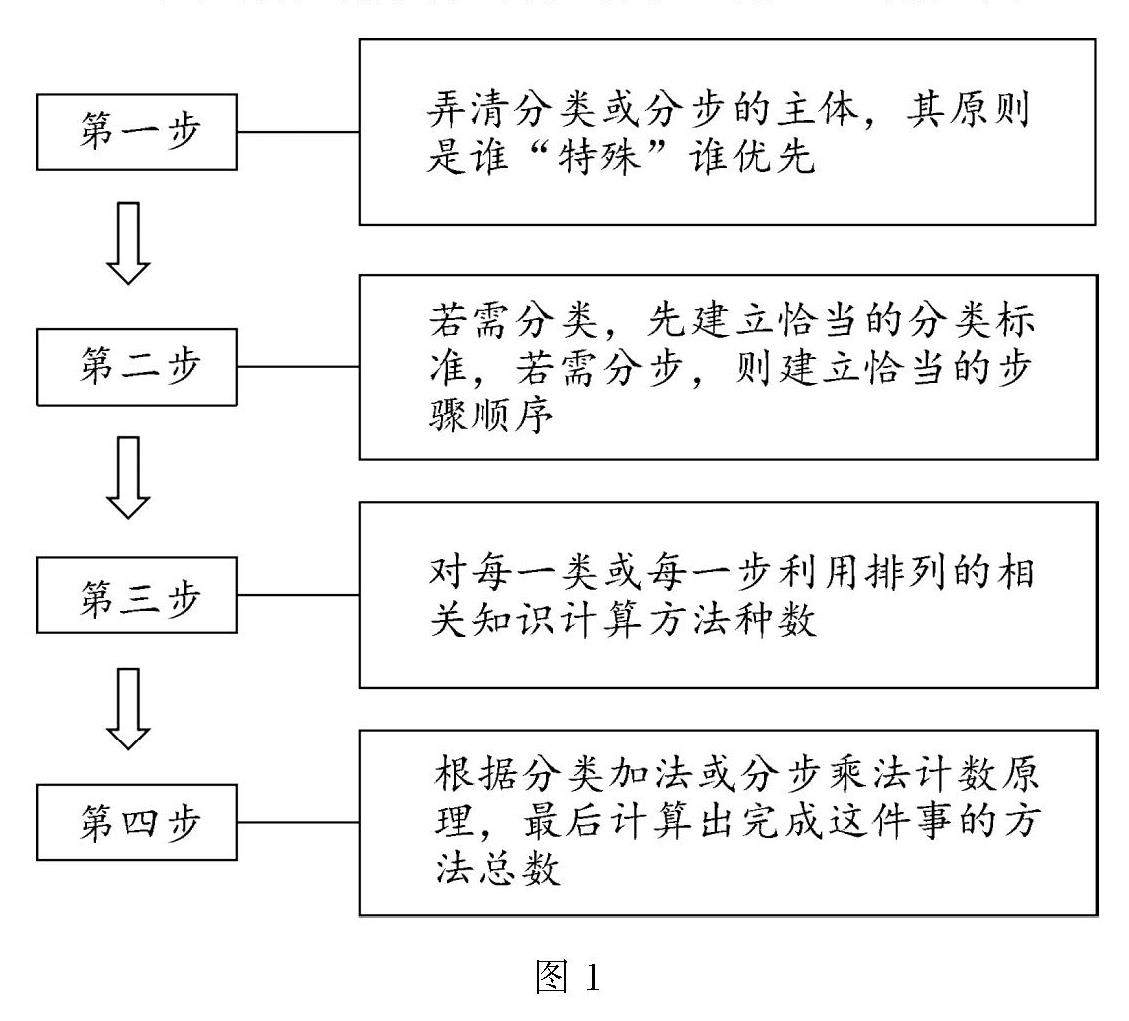
基础精讲 | 排列、组合在实际问题中的应用探究
基础精讲 | 排列、组合在实际问题中的应用探究
-

基础精讲 | 试从不同视角理解辅助角公式的由来
基础精讲 | 试从不同视角理解辅助角公式的由来
-

基础精讲 | 直线方向向量与平面法向量教学课例
基础精讲 | 直线方向向量与平面法向量教学课例
-

基础精讲 | “大单元教学”理念下提升学生核心素养的策略
基础精讲 | “大单元教学”理念下提升学生核心素养的策略
-

基础精讲 | 例谈椭圆中离心率问题的常用二级结论及教学建议
基础精讲 | 例谈椭圆中离心率问题的常用二级结论及教学建议
-

基础精讲 | 立体几何中动点轨迹常见问题及解题策略
基础精讲 | 立体几何中动点轨迹常见问题及解题策略
-

例题精讲 | 浅谈一道圆锥曲线点对称问题的解题方法
例题精讲 | 浅谈一道圆锥曲线点对称问题的解题方法
-

例题精讲 | 从一道大小比较题目的解决看数学思维之美
例题精讲 | 从一道大小比较题目的解决看数学思维之美
-

例题精讲 | 一道圆锥曲线角最大值问题的解法探究
例题精讲 | 一道圆锥曲线角最大值问题的解法探究
-

例题精讲 | “三招”解决一道解三角形长度比值问题
例题精讲 | “三招”解决一道解三角形长度比值问题
-

例题精讲 | 例析同构法在高中数学中的应用
例题精讲 | 例析同构法在高中数学中的应用
-

例题精讲 | 学例谈异面直线的距离解题策略
例题精讲 | 学例谈异面直线的距离解题策略
-

例题精讲 | 例谈同构法在高中数学解题中的应用
例题精讲 | 例谈同构法在高中数学解题中的应用
-
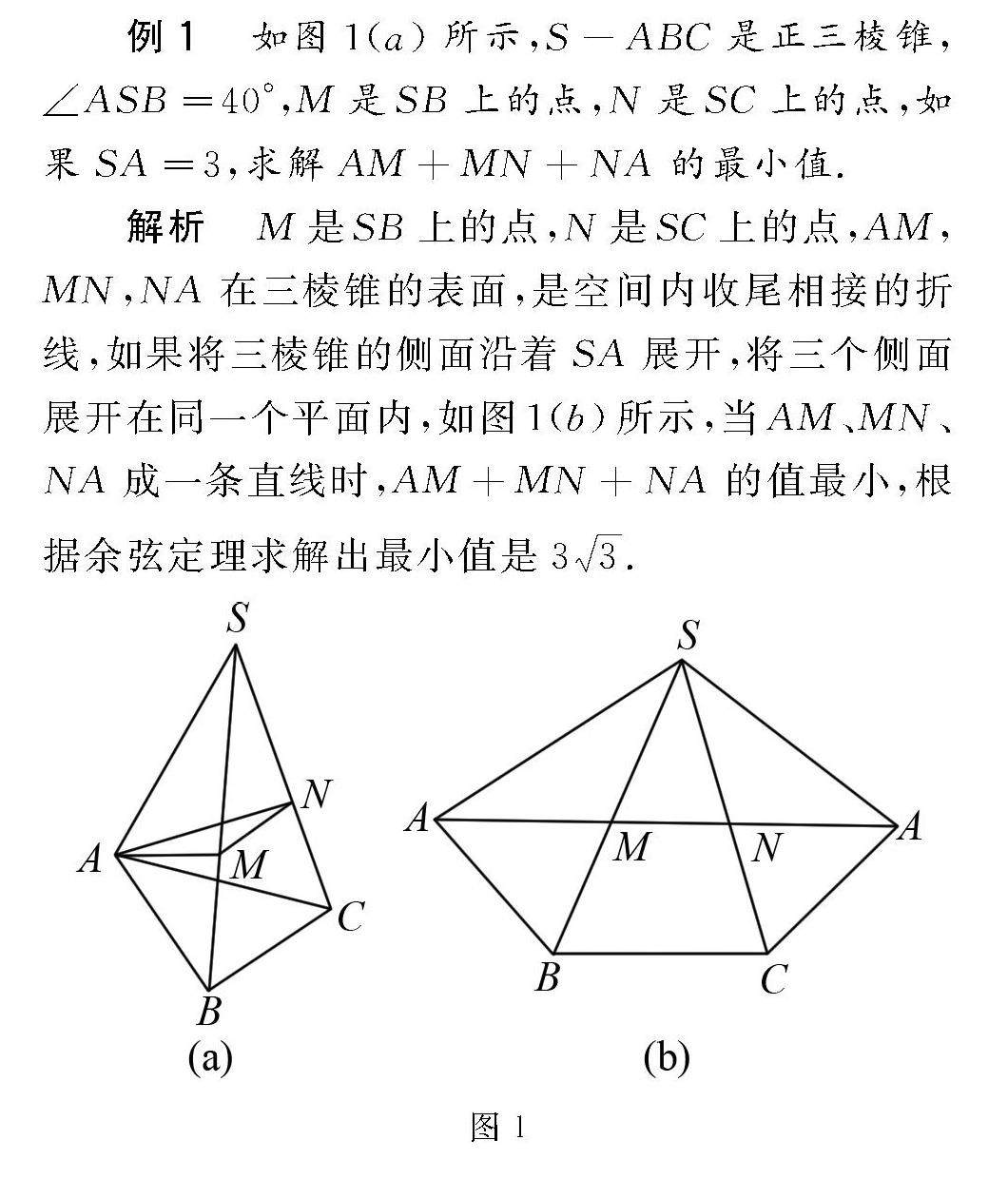
解题技巧 | 借助化归思想,解答数学难题
解题技巧 | 借助化归思想,解答数学难题
-

解题技巧 | 巧借抽象函数结构,妙构特殊函数模型
解题技巧 | 巧借抽象函数结构,妙构特殊函数模型
-

解题技巧 | 函数不等式的三种解题技巧
解题技巧 | 函数不等式的三种解题技巧
-

解题技巧 | “不动”点“妙”解数列通项
解题技巧 | “不动”点“妙”解数列通项
-

解题技巧 | 椭圆与双曲线共焦点的离心率问题解决策略
解题技巧 | 椭圆与双曲线共焦点的离心率问题解决策略
-

解题技巧 | 高中数学解题教学中学生高阶思维能力的培养
解题技巧 | 高中数学解题教学中学生高阶思维能力的培养
-

解题技巧 | 直线与圆位置关系问题的解题技巧
解题技巧 | 直线与圆位置关系问题的解题技巧
-

解题技巧 | 如何解答高中数学立体几何题
解题技巧 | 如何解答高中数学立体几何题
-

解题技巧 | 高中数学的主要最值问题及解题方法探讨
解题技巧 | 高中数学的主要最值问题及解题方法探讨
-

解题技巧 | 高中数学解题中分类讨论思想的运用
解题技巧 | 高中数学解题中分类讨论思想的运用
-

解题技巧 | 立足圆锥曲线定义巧用几何运算解析探索
解题技巧 | 立足圆锥曲线定义巧用几何运算解析探索
-

高考高分之路 | 一道2023年全国高考试题的再探究
高考高分之路 | 一道2023年全国高考试题的再探究
-
优化课堂方法 | 新课标下高中数学课堂存在的问题及改进策略
优化课堂方法 | 新课标下高中数学课堂存在的问题及改进策略
-
优化课堂方法 | 高中数学教学中的创新教学方法探究
优化课堂方法 | 高中数学教学中的创新教学方法探究
-
优化课堂方法 | 高中数学教学中问题导学法的应用建议
优化课堂方法 | 高中数学教学中问题导学法的应用建议
-
优化课堂方法 | 高中数学“问题—互动”教学的探索与实践
优化课堂方法 | 高中数学“问题—互动”教学的探索与实践
-
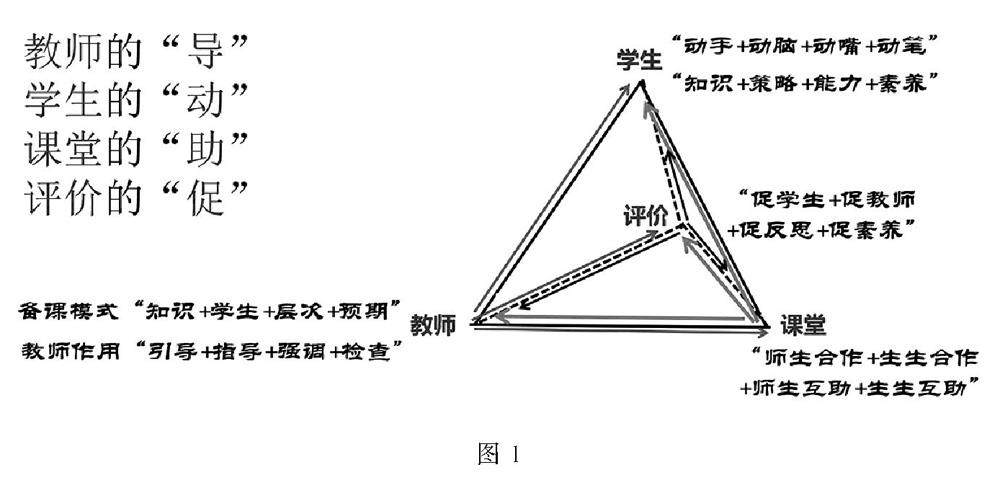
优化课堂方法 | “四位一体”教学模式在高中数学教学中的研究
优化课堂方法 | “四位一体”教学模式在高中数学教学中的研究
-

教学思想实践 | 新高考背景下高中数学复习课之微专题策略
教学思想实践 | 新高考背景下高中数学复习课之微专题策略
-

教学思想实践 | 利用“六何”深度学习法指导课堂教学
教学思想实践 | 利用“六何”深度学习法指导课堂教学
-
教学思想实践 | 大单元视域下的抽象思维在课堂教学的实践
教学思想实践 | 大单元视域下的抽象思维在课堂教学的实践
-

教学思想实践 | 分层分组合作教学的课堂教学时机初探
教学思想实践 | 分层分组合作教学的课堂教学时机初探
-
教学经验交流 | 新课程下高中数学教学中如何培养学生的解题能力
教学经验交流 | 新课程下高中数学教学中如何培养学生的解题能力
-

教学经验交流 | 微专题引领二轮复习 函数思想解范围问题
教学经验交流 | 微专题引领二轮复习 函数思想解范围问题
-
教学经验交流 | 高三数学复习过程中的实践与反思
教学经验交流 | 高三数学复习过程中的实践与反思
-

核心素养培养 | 基于核心素养的高中数学文化渗透浅析
核心素养培养 | 基于核心素养的高中数学文化渗透浅析
-
核心素养培养 | 基于学科核心素养的高中数学单元教学模式探讨
核心素养培养 | 基于学科核心素养的高中数学单元教学模式探讨
-
核心素养培养 | 核心素养下高中数学教学模式探究
核心素养培养 | 核心素养下高中数学教学模式探究
-
核心素养培养 | 中职数学课堂教育核心素养的培养
核心素养培养 | 中职数学课堂教育核心素养的培养
-
核心素养培养 | 核心素养背景下的数学解题教学策略
核心素养培养 | 核心素养背景下的数学解题教学策略
-
核心素养培养 | 高中数学逻辑推理素养的生成意义与教育方法研究
核心素养培养 | 高中数学逻辑推理素养的生成意义与教育方法研究
-
学生培养研究 | 新高考背景下数学教学中培养学生逻辑推理能力的研究
学生培养研究 | 新高考背景下数学教学中培养学生逻辑推理能力的研究
-
学生培养研究 | 高中数学解题过程中学生反思能力的培养
学生培养研究 | 高中数学解题过程中学生反思能力的培养
-
学生培养研究 | 简谈高中生数学解题及学习能力提高的策略
学生培养研究 | 简谈高中生数学解题及学习能力提高的策略
-
教育技术与数学融合 | 数学课堂教学中信息技术的多元化运用分析
教育技术与数学融合 | 数学课堂教学中信息技术的多元化运用分析
过往期刊
更多-

数理天地(高中版)
2024年24期 -

数理天地(高中版)
2024年23期 -

数理天地(高中版)
2024年22期 -

数理天地(高中版)
2024年21期 -

数理天地(高中版)
2024年20期 -

数理天地(高中版)
2024年19期 -

数理天地(高中版)
2024年18期 -

数理天地(高中版)
2024年17期 -

数理天地(高中版)
2024年16期 -

数理天地(高中版)
2024年15期 -
数理天地(高中版)
2024年14期 -

数理天地(高中版)
2024年13期 -

数理天地(高中版)
2024年12期 -

数理天地(高中版)
2024年11期 -

数理天地(高中版)
2024年10期 -

数理天地(高中版)
2024年09期 -

数理天地(高中版)
2024年08期 -

数理天地(高中版)
2024年07期 -

数理天地(高中版)
2024年06期 -

数理天地(高中版)
2024年05期 -

数理天地(高中版)
2024年04期 -

数理天地(高中版)
2024年03期 -

数理天地(高中版)
2024年02期 -

数理天地(高中版)
2024年01期










 登录
登录