目录
快速导航-
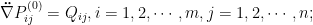
| 混合曲面的改进GS-PIA算法
| 混合曲面的改进GS-PIA算法
-

| CAD网格模型的逆向CSG建模
| CAD网格模型的逆向CSG建模
-
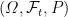
| Heston随机波动率与双指数跳扩散组合模型的双币种幂期权定价
| Heston随机波动率与双指数跳扩散组合模型的双币种幂期权定价
-
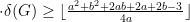
| 孤立韧度与分数 (g,f) -因子
| 孤立韧度与分数 (g,f) -因子
-
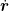
| 星型网络的1-额外3-分支连通性
| 星型网络的1-额外3-分支连通性
-
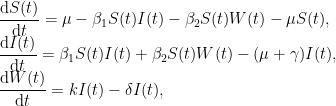
| 具有非局部扩散的霍乱模型的动力学分析
| 具有非局部扩散的霍乱模型的动力学分析
-
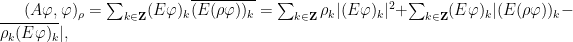
| Schrodinger格点系统在加权空间中的随机吸引子与随机指数吸引子
| Schrodinger格点系统在加权空间中的随机吸引子与随机指数吸引子
-
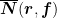
| Fermat型高阶复微分-差分方程的超越整函数解
| Fermat型高阶复微分-差分方程的超越整函数解
-
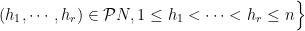
| 泛Clifford分析中的k.-向量正则函数与相关算子的性质
| 泛Clifford分析中的k.-向量正则函数与相关算子的性质















 登录
登录